NFA - DFA DÖNÜŞÜMÜ

DFA

Sonlu otomatların özel bir halidir. Bu özel hal aşağıdaki 3 durumu içermelidir:
1. Her durumdan (State) gidilecek koşulun tek bir durum göstermesi. Yani bir durumda başka duruma geçerken bir kelime ile sadece bir duruma gidilebilmesi
2. Herhangi bir girdi için, tek bitiş durumunun (final state) kabul edilmesi (birden fazla bitiş durumunun aynı anda kabul edilmemesi)
3. Lambda (veya epsilon) kelimesinin durumlar arası geçişte yer almaması

NFA

DFA'nın tersine her durumdan gidişin karışık olduğu ve her durum için bir sonraki kelimede nereye gidileceğinin belirli olmadığı otomatlardır.
Basitçe DFA kurallarına uymayan bütün otomatlar NFA olarak adlandırılabilir.

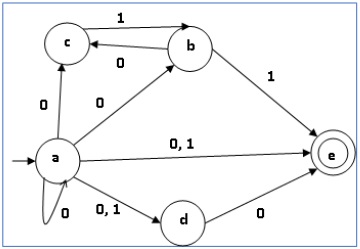
Yukarıda bulunan görselde birden çok seçenek mevcuttur bir komut için. Bu nedenle bu belirsizlikleri ortadan kaldırmak için bir algoritma gerekli

ALGORİTMA/ÖRNEK

Input - NFA
Output - DFA
Adım 1 - Verilen NFA verilerinden bir durum tablosu oluşturun.

q δ(q,0) δ(q,1)
->a {a,b,c,d,e} {d,e}
b {c} {e}
c ∅ {b}
d {e} ∅
*e ∅ ∅
Adım 2 - Alfabede bulunan ihtimaller dahilindeki inputların altında boş bir durum tablosu oluşturun DFA için.
Adım 3 - Tıpkı NFA'da olduğu gibi DFA için başlangıç durumunu q0 olarak ya da bir ok işareti(->) ile işaretleyin.
Adım 4 - Tüm olası durumların kombinasyonunu {Q0, Q1,... , Qn} yazınız.
Adım 5 - Giriş alfabesi sütunlarının altında yeni bir DFA durumu oluşturduğumuzda, 4.adımı tekrar uygulamamız gerekir, aksi takdirde 6.adıma geçin.
Adım 6 - NFA'nın son durumlarından herhangi birini içeren kümeler, eşdeğer DFA'nın son durumlarıdır.
q δ(q,0) δ(q,1)
->[a] [a,b,c,d,e] [d,e]
*[a,b,c,d,e] [a,b,c,d,e] [b,d,e]
*[d,e] [e] ∅
*[b,d,e] [c,e] [e]
*[e] ∅ ∅
*[c, e] ∅ [b]
[b] [c] [e]
[c] ∅ [b]

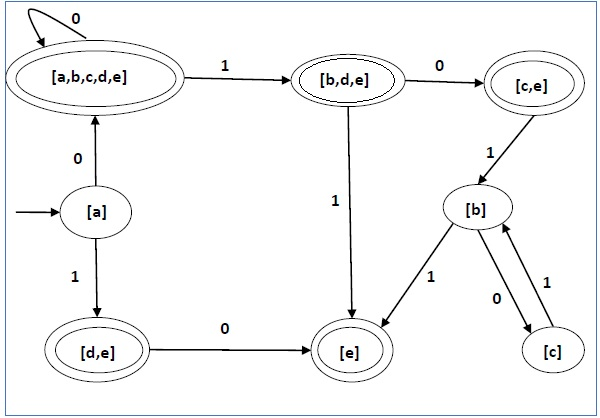
Tablonun bu hale gelmesiyle diyagramımız bu hale gelir:(Uygulama Linki)

Ref: DFA
Ref: NFA
Ref: Dönüşüm Kuralları